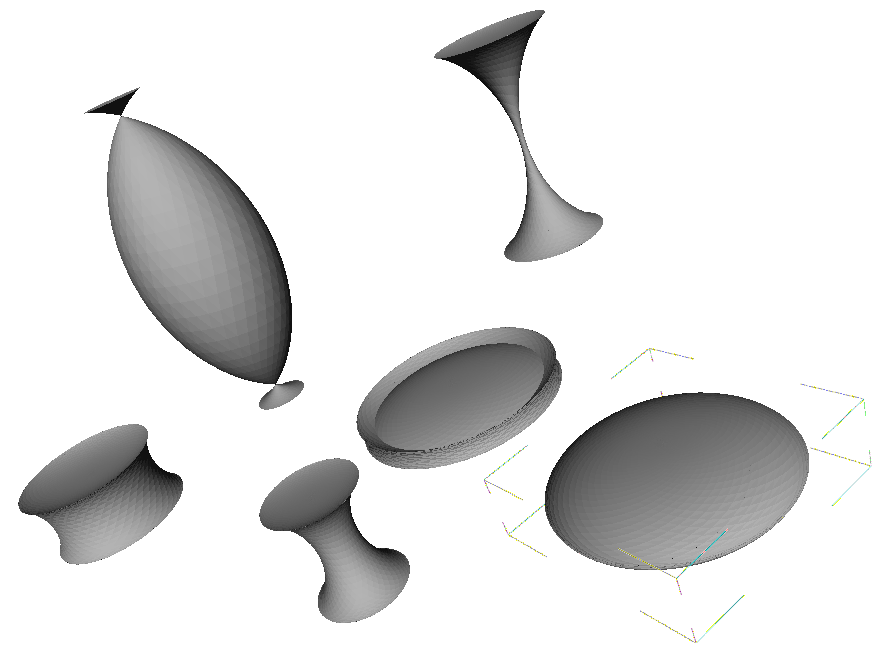
Repozitář STL modelů
Minimální plochy jsou plochy nejmenšího obsahu mezi všemi plochami s danou hranicí (Lagrange). Mohou být definovány i jako plochy s konstantní střední křivostí (Monge). Model představuje část minimálních plochy, kterou nalezl roku 1835 německý matematik Heinrich Scherk (1798--1885). Je to jediná minimální plocha, která je translační, čili vzniklá posunem jedné křivky podél druhé. Obě křivky jsou v tomto případě grafy funkce y = ln cos x.
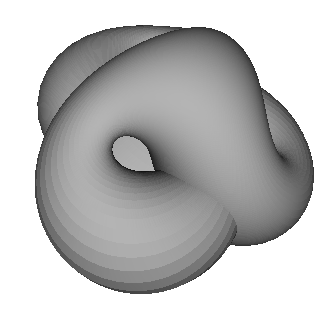
Boyova plocha v Bryant–Kusnerově parametrizaci je plocha s racionální parametrizací, zkonstruována Robertem Bryantem a Robem Kusnerem v roce 1987. Plocham s racionální parametrizací odpovídají integrály vyjádřitelné v elementárních funkcích. S výjimkou kvadrik, běžné plochy racionální parametrizaci nemají.
Boyovou plochou se rozumí hladké vnoření reálné projektivní roviny do R3. Boyova plocha je (podobně jako Möbiova páska a Kleinova láhev) neorientovatelná (má jen jednu stranu). Poprvé tuto plochu zkonstruoval německý matematik Werner Boy v roce 1901 poté, co jej jeho školitel David Hilbert požádal o důkaz její neexistence. Model sestává ze dvou kusů, aby bylo vidět dovnitř.
Diniho plocha je příkladem pseudosférické plochy, čili plochy záporné konstantní Gaussovy křivosti. Je modelem Lobačevského geometrie. Diniho plochu opisuje křivka zvaná traktrix, vykonává-li šroubový pohyb (čili složení otáčivého a postupného pohybu) podél své asymptoty. Plocha je pojmenována po italském matematiku Ulisse Dini (1845--1918). Její hranicí je šroubovice. Speciálním případem je pseudosféra (přesněji řečeno, jedna její polovina), vznikající při pohybu čistě otáčivém.
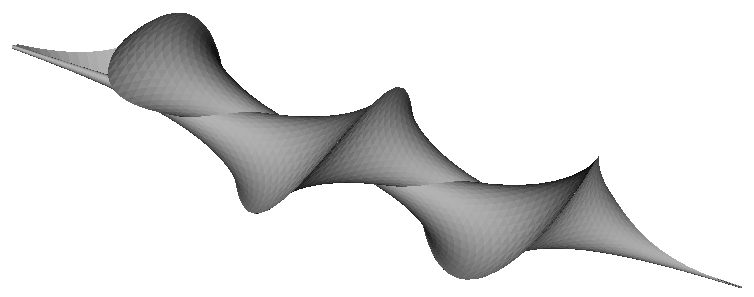
Model představuje sjednocení dvou Diniho ploch, majících společnou hraniční šroubovici. Plocha sama sebe protíná. (Objekt se skládá ze dvou kusu pro efektnejší tisk bez podpor.)
Celou sféru nelze deformovat se zachováním vzdáleností, ale část sféry lze. Příkladem je Sievert-Enneperova plocha. ( V zip souboru naleznete řez pro efektnější tisk bez podpor)
Rozvinutelnou plochou se rozumí plocha nulové Gaussovy křivosti. Je izometrickou deformací části roviny. Můžete se o tom přesvědčit přiložením vhodně tvarovaného kusu papíru. Nejobecnějším typem rozvinutelné plochy je plocha tvořená tečnami k zadané prostorové křivce, která se nazývá generující křivka. Zde je generující křivkou Vivianiho křivka, čili průsečnice koule a válce.
Rozvinutelnou plochou se rozumí plocha nulové Gaussovy křivosti. Je izometrickou deformací části roviny. Můžete se o tom přesvědčit přiložením vhodně tvarovaného kusu papíru. Nejobecnějším typem rozvinutelné plochy je plocha tvořená tečnami k zadané prostorové křivce, která se nazývá generující křivka. Zde je generující křivkou šroubovice.
Veďme řez anuloidem tak, že průnikem anuloidu a kterékoliv roviny vedené kolmo k centrální kružnici je vždy přímka (můžeme si ji představit jako řezný nástroj). Pokud se přímka během oběhu centrální kružnice otočí o 180°, je řezem Möbiova páska. Takový řez nevede k rozdělení anuloidu na dvě části. Pokud se však přímka během oběhu centrální kružnice otočí o 360°, rozpadne se anuloid na dvě části. Ty jsou ovšem vzájemně zapleteny a jednu od druhé nelze odpoutat.
Kuenova plocha je pseudosférickou plochou čili modelem Lobačevského geometrie. Pseudosférické plochy odpovídají řešením sin–Gordonovy rovnice uxy = sin(u), která náleží mezi exaktně řešitelné rovnice, přestože je silně nelineární. Kuenova plocha odpovídá speciálnímu dvousolitonovému řešení. (V zip souboru je jednak celá plocha i jednotlivé řezy pro efekt. tisk bez podpor)
Před zprovozněním GPS lodě pluly a letadla létala podél křivek s konstantní odchylkou od magnetických poledníků. Křivky, které mají konstantní odchylku od poledníků, se nazývají loxodromy. Na modelu vidíme síť loxodrom s odchylkou od poledníků 45 stupňů.
Archimedova projekce je nejen kartografické zobrazení, ale i způsob dělení sféry na křivočará políčka stejného obsahu.
Lorenzův atraktor je fraktál, představující podivný atraktor dynamického systému, odvozeného v roce 1963 americkým matematikem a meteorologem Edwardem Lorenzem (1917--2008) jako zjednodušený model atmosférické konvekce. Atraktor je invariantní podmnožina, k níž jsou přitahována všechna dostatečně blízká řešení. Atraktor je podivný, je-li fraktální.
Mezi dnes téměř zapomenuté plochy, studované v době rozkvětu diferenciální geometrie koncem XIX. století, patřily plochy s konstantním rozdílem mezi hlavními poloměry křivosti. Jednu z nich objevil Rudolf Lipschitz, jehož jméno nese i podmínka existence a jednoznačnosti řešení obyčejné diferenciální rovnice.
Izometrickou deformací plochy se rozumí deformace, při níž se zachovávají vzdálenosti mezi odpovídajícími si body. Je známou, že celou sféru izometricky deformovat nelze. Model představuje izometrickou defomaci sférického pásu vymezeného na sféře dvěma rovnoběžkami stejně vzdálenými od rovníku. Pokud by byl zhotoven z pružného materiálu a rozříznut polorovinou procházející osou symetrie, bylo by možné "svinutím" do sebe získat výchozí sférický pás.
Funkce může být diferencovatelná v každém bodě v každém směru, ale Gâteaux-nediferencovatelná v nějakém bodě. Zde je příklad grafu takovéto funkce RxR -> R.
Ekviareální vzor na sféře je dělení sféry na křivočará políčka stejného obsahu. Jeden netriviální ekviareální vzor vidíme na modelu. Pokrývá jen naznačený pás kolem "rovníku".
Tečná rovina ke grafu Gâteaux diferencovatelné funkce může být větší než graf příslušné derivace. Model znázorňuje graf funkce: RxR -> R, která je Gâteaux diferencovatelná v bodě x, ale tečná rovina ke grafu funkce f v bodě (x,f(x)) se neshoduje s grafem derivace v bodě x.
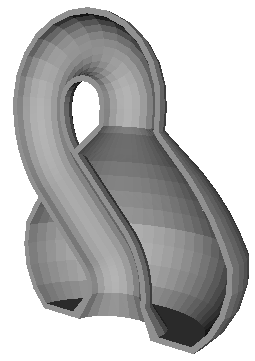
Kleinova láhev je velmi populární příklad plochy v R3, která má jen jednu stranu – nemá oddělený vnitřek a vnějšek. Podle matematiků je neorientovatelná. Na rozdíl od ještě populárnější Möbiovy pásky je navíc uzavřená (nemá okraje ani nesahá do nekonečna).
Dvojité kyvadlo může sloužit k demonstraci chaotického pohybu. Je-li jeden konec upevněn a druhý uveden v setrvačný pohyb, opisuje dosti komplikované trajektorie. Vykazuje též velkou citlivost k malým změnám počátečních podmínek, zejména v blízkosti trajektorií, u kterých dojde k průchodu horní labilní polohou (překlopení). Pohybové rovnice dvojitého kyvadla lze řešit pouze numericky, nikoliv analyticky.
Plochou konstantního astigmatismu rozumíme plochu, vyznačující se konstantním rozdílem hlavních poloměrů křivosti. Model ukazuje výsek plochy konstantního astigmatismu, která je involutou Diniho plochy. Tuto plochu uveřejnil Luigi Bianchi v roce 1892.
Plochou konstantního astigmatismu rozumíme plochu, vyznačující se konstantním rozdílem hlavních poloměrů křivosti. Model demonstruje jednoparametrickou soustavu ploch konstantního astigmatismu, vznikajících jako involuty pseudosféry. Poprvé je popsal Rudolf Lipschitz v roce 1887, vztah k pseudosféře objevil záhy poté Reinhard von Lilienthal. Jsou to jediné rotační plochy konstantního astigmatismu. Všechny jsou ohraničené, některé jsou hladké, jiné nikoli. Není známo, zda existují nerotační ohraničené plochy konstantního astigmatismu. Zde jsou vykresleny vůbec poprvé. Animace ukazuje, jak se von Lilienthalovy plochy mění v závislosti na parametru.
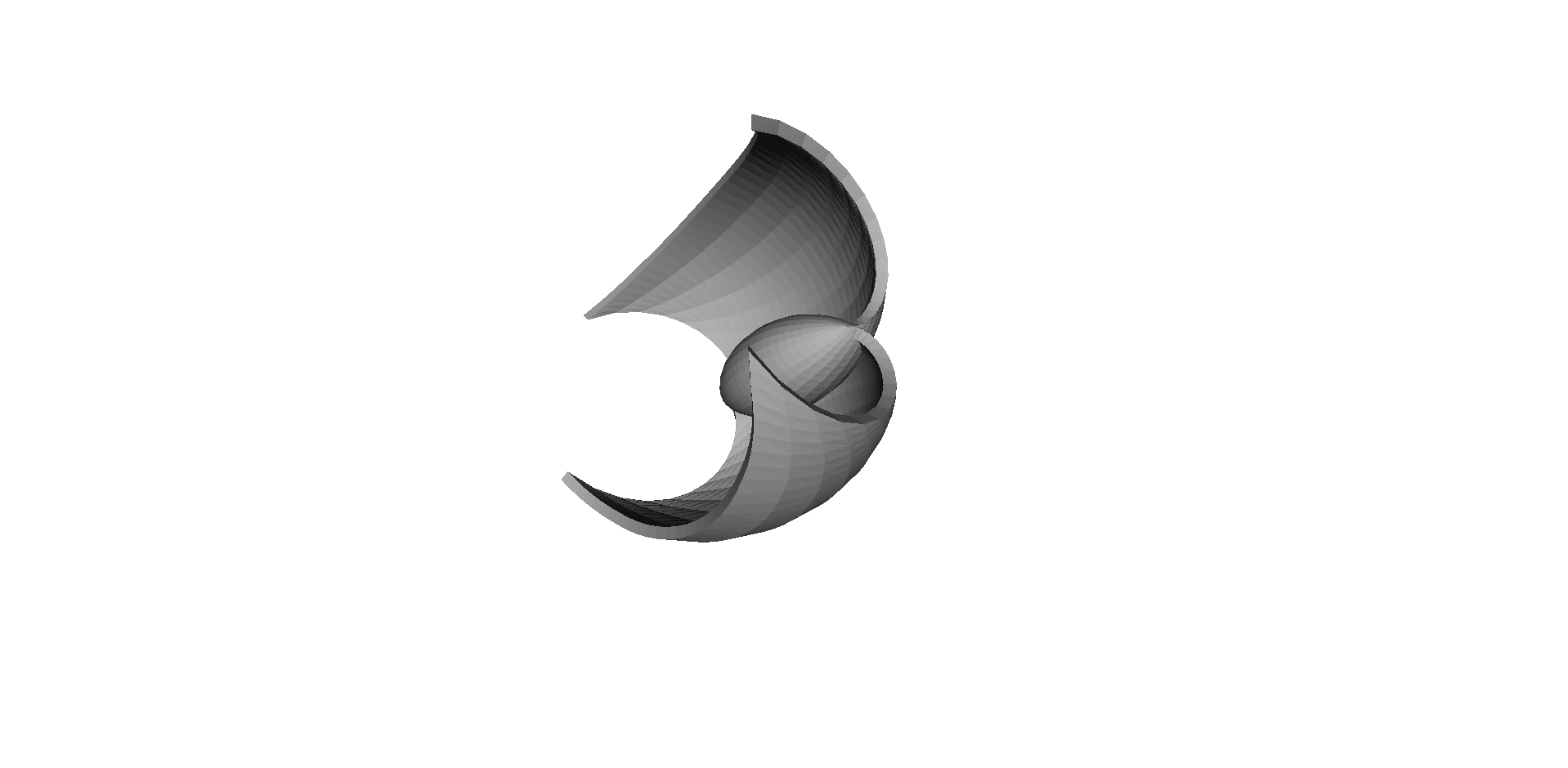
Plocha konstantního astigmatismu publikovaná v roce 2018, objevená na Matematickém ústavu v Opavě. Evolutami této plochy jsou Mindingova tubulární pseudosférická plocha a její Bäcklundova transformace.
Plocha konstantního astigmatismu publikovaná v roce 2018, objevená na Matematickém ústavu v Opavě. Evolutami této plochy jsou Mindingova kónická pseudosférická plocha a její Bäcklundova transformace.
Minimální plocha je plocha nejmenšího obsahu mezi všemi plochami s danou hranicí (Lagrange). Lze ji definovat i jako plochu s konstantní střední křivostí (Monge). Model představuje část minimálních plochy, kterou nalezl roku 1982 brazilský matematik Celso José da Costa. Costova plocha je neohraničená a neprotíná sama sebe, což před Costovým objevem splňovaly pouze rovina, katenoid a helikoid.
Minimální plocha je plocha nejmenšího obsahu mezi všemi plochami s danou hranicí (Lagrange). Lze ji definovat i jako plochu s konstantní střední křivostí (Monge).
Jedna ze tří částí modelu tzv. křivkového přeboru. Tento přebor demonstruje fakt, že brachistochrona je křivka spojující dva body, po které se hmotný bod dostane z počátečního klidu v jednom bodě do druhého působením homogenního gravitačního pole za nejkratší dobu. Do celistvého a funkčního modelu nutno ještě vytisknout modely "Přímka" a "Křivka" . (Animace-zdroj: https://cs.wikipedia.org/wiki/Brachistochrona)
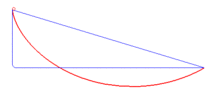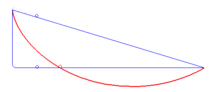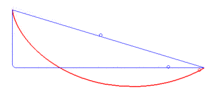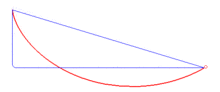
Jedna ze tří částí modelu tzv. křivkového přeboru. Tento přebor demonstruje fakt, že brachistochrona je křivka spojující dva body, po které se hmotný bod dostane z počátečního klidu v jednom bodě do druhého působením homogenního gravitačního pole za nejkratší dobu. Do celistvého a funkčního modelu nutno ještě vytisknout modely "Brachistochrona" a "Křivka" . (Animace-zdroj: https://cs.wikipedia.org/wiki/Brachistochrona)
Jedna ze tří částí modelu tzv. křivkového přeboru. Tento přebor demonstruje fakt, že brachistochrona je křivka spojující dva body, po které se hmotný bod dostane z počátečního klidu v jednom bodě do druhého působením homogenního gravitačního pole za nejkratší dobu. Do celistvého a funkčního modelu nutno ještě vytisknout modely "Přímka" a "Brachistochrona" . (Animace-zdroj: https://cs.wikipedia.org/wiki/Brachistochrona)
Ekviareální síť je tvořena křivočarými políčky stejného obsahu. Jedna netriviální ekviareální síť je zde zobrazena .
Ekviareální síť je tvořena křivočarými políčky stejného obsahu. Jedna netriviální ekviareální síť je zde zobrazena .
Pomůcka pro experimentální ověření správnosti výpočtu objemu tělesa vytvořeného rotací plochy vymezené třemi křivkami \(y=0,\; y=(\frac{2}{3}x-\frac{1}{3})^2-1,\;y=\frac{16}{9}x-\frac{8}{9}\) kolem osy \(x=0\)
Pomůcka pro experimentální ověření správnosti výpočtu objemu tělesa vytvořeného rotací křivky \(y=\frac{9}{10}x^2-4x+5,\;x=\frac{1}{2}..5\) kolem osy \(y=0\)
LICENCE
Soubor, který se chystáte stáhnout, smíte užít jen pro vlastní nevýdělečnou potřebu. Každé jiné užití podléhá schválení Slezskou univerzitou v Opavě, která je nositelem autorských práv. Soubor nesmíte za žádných okolností dále šířit.
Každé užití tohoto souboru je výlučně na vlastní riziko. Slezská univerzita v Opavě nenese žádnou odpovědnost za výsledek či následek. Souhlas s výše uvedeným projevíte stisknutím tlačítka Souhlasím.
